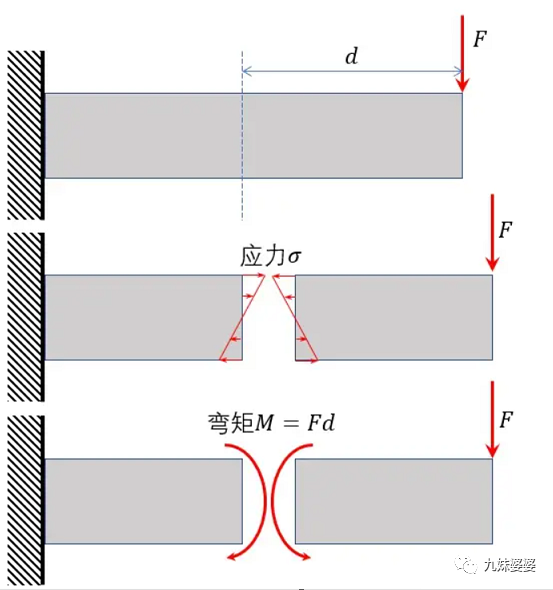
起重机主梁弯矩与剪力

1、什么是弯矩

我们从最基本的开始，初中都学过杠杆原理，人教版《物理》八年级下册第12章「简单机械」第1节「杠杆」里就提到过：

「力×力臂」这种计算方法是初中已经讲过的，这其实就是力矩的计算。我们通过这个物理量来研究物体的旋转，度量产生旋转的作用效果。力矩越大，对旋转产生的影响就越大。

力矩仍然是力产生的，力是实际的相互作用，它的作用效果有平动和转动两种。

力对平动的作用效果，我们用'力的大小'来衡量，力对转动的作用效果，我们用「力矩」来衡量。

2、弯矩与剪力的计算步骤

大学力学课程中规定，弯矩下部受拉为正（上部受压），上部受拉为负（下部受压），这是力学领域的定义。

但在土木建筑学领域，为了让弯曲方向与变形方向一致，通常上部受压的梁受到弯矩，画在负方向。在起重机行业，通常采用土建领域达到画法，即上部受压时，弯矩图画在下方。

画弯矩图（或剪力图）是有技巧的，或者说快捷途径的。但各种技巧都是建立在了解结构受力，对于各种作用在结构上的荷载使结构产生的反力与内力形式都能了然于胸的基础上，才会省略一些相对来说不是很必要的步骤。

截面法是一种结构力学中常用的分析方法，我们还是可以用力矩平衡求得支座反力后利用截面法求得弯矩方程，根据弯矩方程绘制弯矩图，剪力同样道理，弯矩和剪力是存在着微分关系，对弯矩求导就是剪力。

（1）由平衡方程计算支反力；

（2）选择截面：截面通常位于结构中的一个特定位置，如集中力的附近。

（3）根据集中力、集中力偶划分剪力、弯矩的变化区间；

（4）根据变化区间建立剪力与弯矩方程；

（5）绘制剪力图、弯矩图。

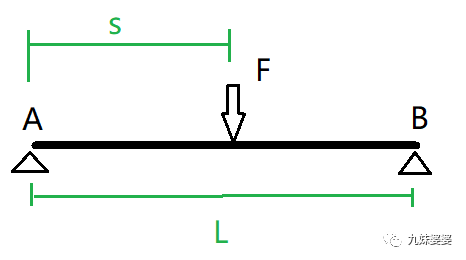
3、集中载荷作用下简支梁弯矩和剪力方程推导

以常见的集中载荷作用下的简支梁（起重机主梁近似为简支梁结构）为例，介绍一下截面法求解弯矩和剪力的过程。

（1）计算支反力：

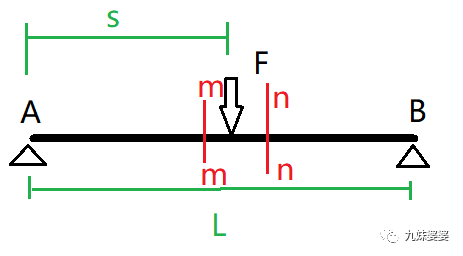
在集中载荷左侧选择任一截面m-m；在集中载荷右侧选择任一截面n-n

设定截面到支点A的距离为x，根据截面的位置，x有两个变化区间：

区间1：0≤x≤s

区间2：s≤x≤L

对截面m-m处，根据力的平衡和力矩平衡进行分析：

m-m截面处的剪力：FS=FA=F(L-s)/L

m-m截面处的弯矩：M=FAx=F(L-s)x

对截面n-n处，根据力的平衡和力矩平衡进行分析：

n-n截面处的剪力：FS=FB=Fs/L

n-n截面处的弯矩：M=FAx=F(L-s)x

（5）绘制剪力图、弯矩图

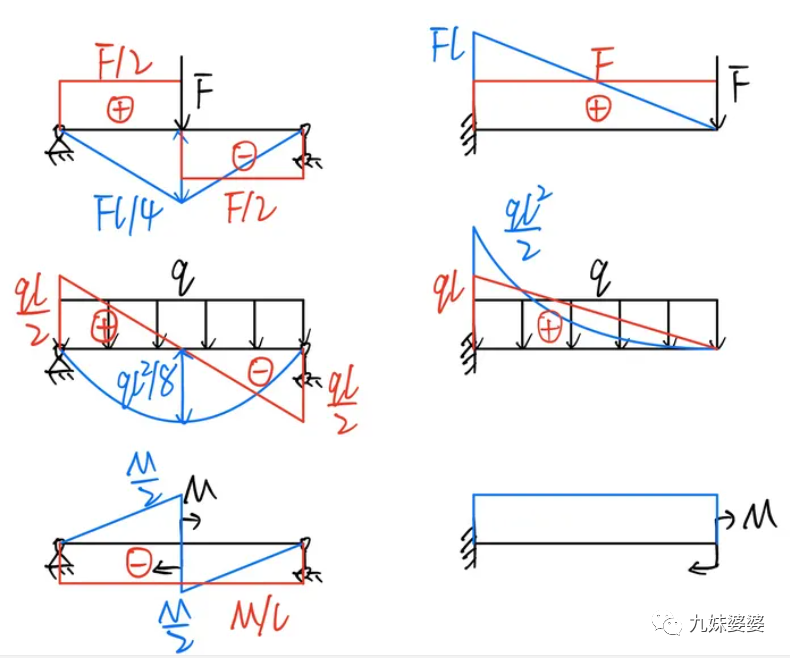
4、常见的弯矩图和剪力图

5、起重机械检验师考题的解析

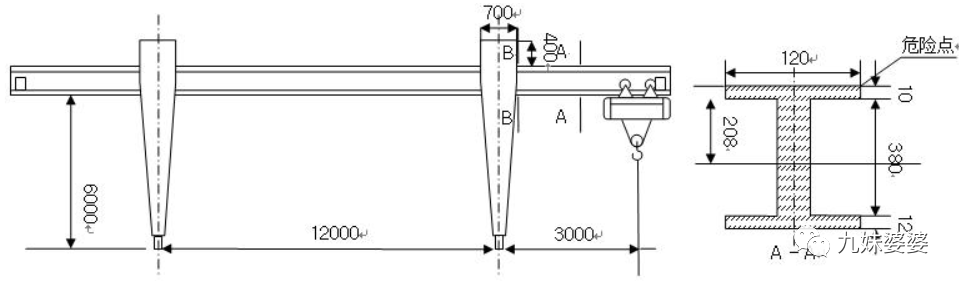
5.1   检验师考题1

问：（1）画出满载葫芦在跨内距左大车轮中心S/4处时，主梁的弯矩图和剪力图（其他问题的解答在随后几天给出解析）。

解析：首先说明一点，检验师考题不会考大家剪力方程和弯矩方程，最多考大家能不能画出来剪力图和弯矩图，为了给大家讲明白剪力图和弯矩图是怎么来的，我给大家把剪力方程和弯矩方程列出来。这道题用S表示跨度，和原题保持一致，注意和前面分析对应起来。

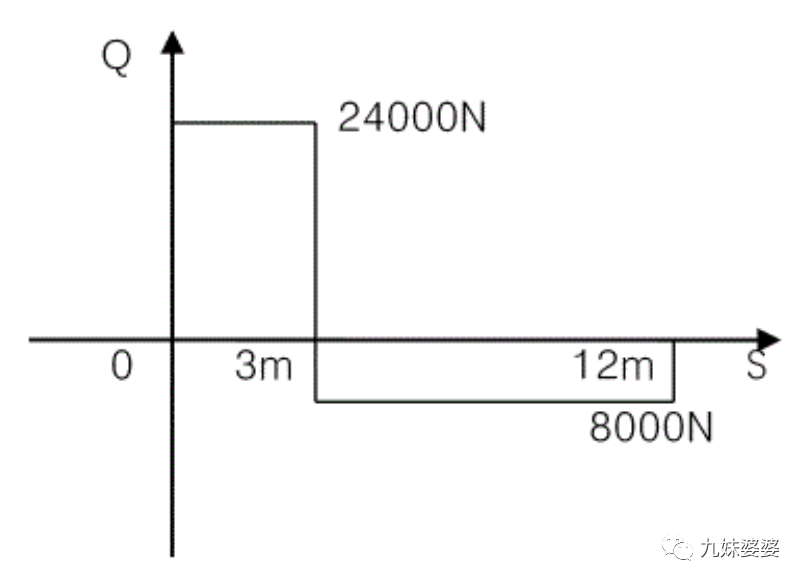
先把有用信息提出来，集中载荷：
F=（3000+200）×10=32000 N

跨度：S=12 m

剪力方程：

由剪力方程画出剪力图

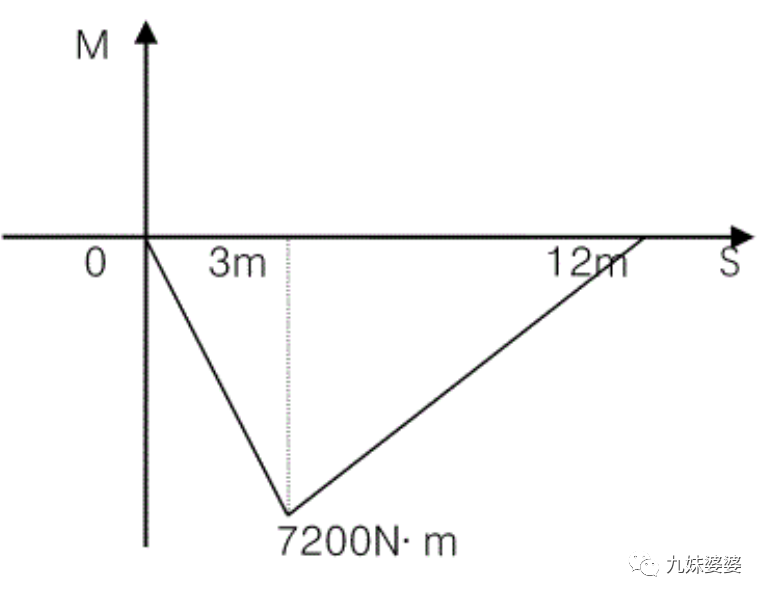
弯矩方程：

由弯矩方程画出弯矩图

5.2   检验师考题2

一型号规格为QD32-22.5A5通用桥式起重机主梁结构如图所示，该起重机技术资料显示：薄壁箱形结构主梁，小车自重为12t，用吊钩作业，整机采用简单控制系统能达到中等定位精度，主梁最大截面惯性矩I=1.5×10⁹ mm⁴，材质为Q235,弹性横量E=2.1×18⁶ N/mm²，g=10 m/s²，请问：

（1）最大弯矩发生在主梁什么位置？计算主梁最大弯矩值？画出弯矩图（其他问题的解答在随后几天给出解析）。

解析：先把有用信息提出来，集中载荷：

F=（32+12）×10=440 kN

跨度：S=22.5 m

这道题用S表示跨度

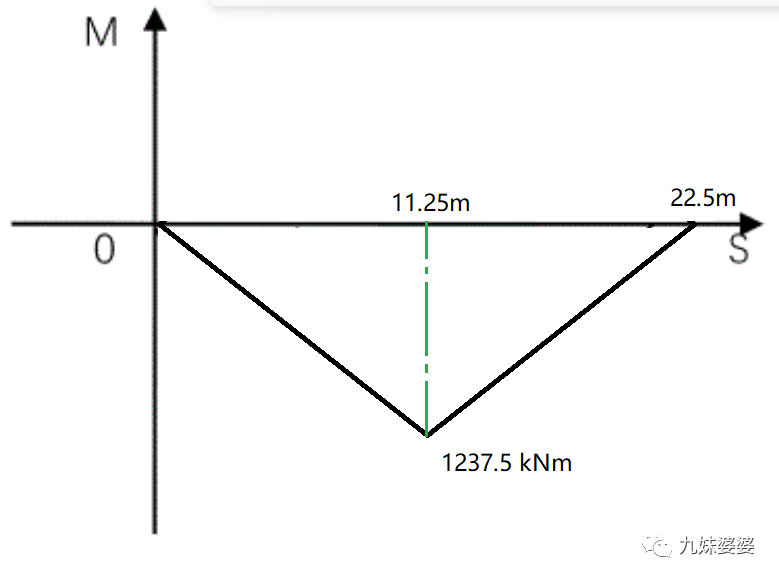
由本文第三节分析，当集中载荷作用在跨中，弯矩最大。

不过要注意一点，这是通用桥式起重机，所有的载荷由两根主梁承担，

计算任一根主梁的弯矩可作为该起重机的弯矩。

最大的弯矩为：

Mmax=440×22.5/8=1237.5 kNm

如果熟练，不用再推算弯矩方程。此时可以直接画出弯矩图。

注意：这道题是一个错题，再说的直接一点，2019年之前的起重机械检验师考题，所有涉及弹性模量和惯性矩的数据全是错的，是出题组的专家基础力学知识薄弱导致的。这一点有机会在和大家细谈。